Свойства определенного интеграла

1. Значение определенного интеграла не зависит от обозначения переменной интегрирования, т.е.

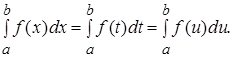
Это утверждение непосредственно следует из определения интеграла как числа, равного пределу интегральных сумм. В случае неотрицательной подинтегральной функции утверждение особенно очевидно, так как площадь соответствующей криволинейной трапеции не зависит от обозначения оси абсцисс.

2. Определенный интеграл меняет знак при перестановке пределов интегрирования, т.е. при :

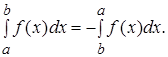
Доказательство. Согласно формуле 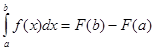имеем:

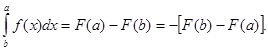
3. Постоянный множитель можно выносить за знак определенного интеграла, т.е.

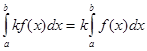, для любого числа k.

Доказательство. Действительно, для любого разбиения Т промежутка ОХ от до и любого выбора точек

.

Переходя к пределу при стремлении шага разбиения к нулю, получаем:

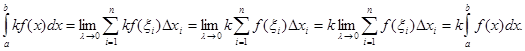
4. Определенный интеграл от суммы двух функций f1(x) и f2(x) равен сумме определенных интегралов от слагаемых, т.е.

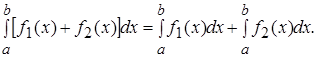
Доказательство. Действительно, для любого разбиения промежутка от до и любого выбора точек

Так как ,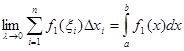

,

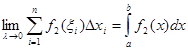то получаем что

.

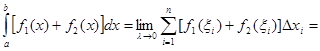
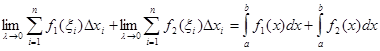5. Если отрезок [a,b] разбит точкой С на две части [a,c] и [c,b], то

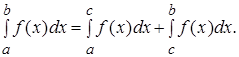
Доказательство. Так как интеграл 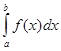, равный пределу интегральных сумм, не зависит от применяемого при составлении интегральных сумм способа разбиения отрезка на части, можно рассматривать только те разбиения, в которых точка входит в качестве точки деления. Тогда

,

где и - суммы, соответствующие отрезкам деления, попавшим соответственно на отрезки и .

Переходя к пределу, при стремлении шага разбиения отрезка к нулю, получим:

,

,

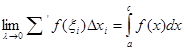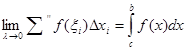а значит,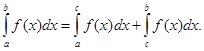

6. Если всюду на отрезке функция , то

.

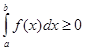Доказательство. В самом деле, любая интегральная сумма

для функции на отрезке неотрицательна, так как

, , .

Переходя к пределу в неравенстве , получаем .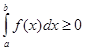

7. Если всюду на отрезке , то .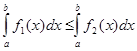

8. Для функции , заданной на отрезке, имеет место неравенство

Статьи по теме:

Разработка сводно-тематического плана подготовки специалиста
Сводно-тематический план должен включать в себя тематику специальных дисциплин («Спецтехнология», «Производственное обучение» и т.д.), регламентировать последовательность изучения тем и количество, отводимого на их изучение времени, по семестровое членение учебных курсов, отражать формы обучения (у ...

Своеобразие восприятия сказочных персонажей художественной литературы дошкольниками с нарушением интеллекта
В программе воспитания в специализированном детском саду предусмотрено знакомство детей с художественной литературой. Им рассказывают и читают народные сказки и потешки, детские произведения отечественных и зарубежных писателей. Знакомство аномальных детей с художественной литературой является мощн ...

Особенности применения соревновательного метода при обучении двигательному действию
Соревновательный метод является не лучшим средством обучения двигательному действию, так как этот достаточно сложный процесс требует сосредоточения внимания именно на выполнении техники двигательного действия, выполнения четких и точных движений. Особенно нецелесообразно применять его на первом и в ...