Понятие определенного интеграла

Пусть -функция, непрерывная на отрезке . Разобьем отрезок на n-частичных(элементарных) отрезков . В каждом из этих последовательных отрезков выберем точку . Составим сумму вида

. (1)

Эта сумма называется интегральной для функции .

Определение1. Интегральной суммой данной функции на данном отрезке называется сумма парных произведений длин элементарных отрезков на значения функции в выделенных точках последних.

Значение интегральной суммы зависит: 1) от способа разбиения основного отрезка на элементарные и 2) от выбора промежуточных точек x в этих последних.

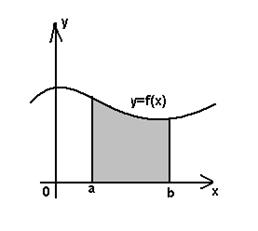
Если и ,то геометрически интегральная сумма представляет собой площадь ступенчатой фигуры, состоящей из n прямоугольников, основания которых есть элементарные отрезки , а высоты равны выбранным значениям функции. В общем случае интегральная сумма есть алгебраическая сумма площадей этих прямоугольников.

Пусть число точек деления n неограниченно растет и ; если при этом интегральная сумма имеет конечный предел, не зависящий от способа дробления отрезка на частичные отрезки и от выбора точек в них, то последний называется определенным интегралом от функции .

Определение 2. Определенным интегралом от данной функции на данном промежутке (или в пределах от a до b) называется предел соответствующей интегральной суммы при условии, что длина наибольшего элементарного отрезка подразбиения стремится к нулю, т.е.

. (2)

Числа a и b называются соответственно нижним и верхним пределами интегрирования определенного интеграла (2). Заметим, что знак интеграла есть стилизованная сумма.

Функции , для которых существуют пределы интегральных сумм, называются интегрируемыми на соответствующем отрезке. Приведем без доказательства теорему об интегрируемости непрерывной функции.

Статьи по теме:

Диагностика уровня сформированности познавательного интереса у детей старшего дошкольного возраста при ознакомлении с неживой природой
В процессе экспериментирования дошкольник получает возможность удовлетворить присущую ему любознательность, почувствовать себя ученым, исследователем, первооткрывателем. Проводимые эксперименты с различными материалами и предметами (вода, снег, песок, стекло, воздух и т.п.) представляют ребенку воз ...

Образовательное пространство: теоретико-методологический аспект
Крупный вклад в научное осмысление данной проблемы внесли К.Д.Ушинский, В.И.Вернадский, И.Я.Яковлев, Н.К.Крупская, А.С.Макаренко и другие. Создание государственной системы образования тесно связано с именами: К.Н. Вентцеля, А.У. Зеленко, Е.Н. Медынского, С.Т. Шацкого и других. Исследованием специфи ...

Методы обучения глухих дошкольников устной речи
Метод обучения – это система последовательных взаимосвязанных способов работы педагога и обучаемых детей, которые направлены на достижение дидактических задач. В дошкольной сурдопедагогике рассматривается использование общедидактических методов для развития речи глухих детей, такие как наглядные, с ...