Формула Ньютона-Лейбница

Пусть F(x) – любая первообразная для функции f(x) на отрезке [a,b]. Так как первообразные Ф(х) и F(x) отличаются постоянным слагаемым, то имеет место равенство

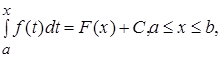
где С- некоторое число.

Подставляя в это равенство значение х=а, будем иметь:

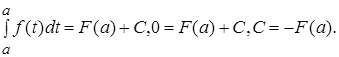
Таким образом, для любого значения х, ,

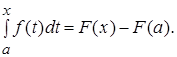
В частности, при x=b получаем:

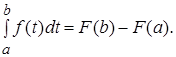
Формула 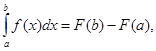(3)

выражающая определенный интеграл от непрерывной функции через неопределенный, называется формулой Ньютона-Лейбница.

Разность F(b)-F(a) принято условно записывать в виде:

или .

Формула (3) или, что то же формула

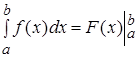
показывает, что определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленных для верхнего и нижнего пределов интегрирования. Формула Ньютона-Лейбница дает простой и удобный метод вычисления определенных интегралов от непрерывных функций, применимый в тех случаях, когда первообразная подинтегральной функции может быть найдена в элементарных функциях. Формула Ньютона – Лейбница обычно записывают в виде

.

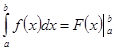Замечание. Удобно расширить понятие интеграла, полагая по определению при . Что

.

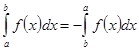При таком соглашении формула Ньютона – Лейбница оказывается верной при произвольных и (в частности ).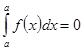

Замена переменной в определенном интеграле

Пусть требуется вычислить определенный интеграл 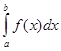от функции f(x), непрерывной на отрезке [a,b]. Имеет место правило замены переменной.

Если: 1) функция непрерывна вместе со своей производной на отрезке с концами () оси Ot;

2) при изменении t от до значение функции не выходит за пределы отрезка [a,b]

3) то

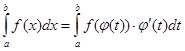
Действительно по формуле Ньютона-Лейбница

,

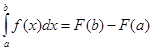Где F(x) – какая-нибудь первообразная для функции f(x) на отрезке [a,b].

Так как при этом функция F() является первообразной для функции , непрерывной на отрезке оси Ot с концами t= и t= , то по той же формуле Ньютона-Лейбница

Статьи по теме:

Организация коммуникации в учебном процессе
В основе коммуникационного процесса в системе традиционного обучения лежит монолог педагога. Педагог с готовыми знаниями идет к учащемуся и, используя систему поощрений и наказаний, заставляет его принять информацию как необходимую и обязательную. Взаимодействие между участниками образовательного п ...

Особенности применения игрового метода на уроке физической культуры
На уроке физической культуры, особенно в младших классах школы игровой метод физического воспитания применяется главным образом в форме подвижных игр. Подвижные игры следует подбирать такие, которые воспитывают у учеников высокие морально-волевые качества и укрепляют здоровье, оказывают содействие ...

Проектирование воспитательной работы в контексте социально-педагогической парадигмы
Развитие современного образовательного пространства представляет собой вариативный процесс, направленный на удовлетворение образовательных потребностей ребенка, общества, государства. Это возможно при условии ориентации образования на социальный заказ, выявляемый в ходе мониторинга социальной среды ...