Задачи, приводящие к понятию определенного интеграла

При решении задачи будем учитывать закон Паскаля, т.е. то, что давление жидкости передается во все стороны одинаково.

Для решения задачи разобьем пластину на частей (малых горизонтальных полосок) прямыми, параллельными свободной поверхности жидкости (т.е. параллельно оси ) и проходящими через точки:

, .

Выделим одну из полосок - ю (на рисунке она заштрихована), находящуюся на глубине . Для достаточно узкой полоски давление во всех ее частях можно считать приближенно одинаковым а саму полоску можно принять за прямоугольник с высотой и основанием, равным нижнему основанию полоски. Легко видеть, что основание прямоугольника зависит от глубины погружения полоски, т.е. будет функцией абсциссы . Обозначим эту функцию , . Таким образом, силу давления на полоску можно вычислить по формуле (*), т.е. имеем:

.

Просуммировав силы давления жидкости на все полоски, найдем некоторое приближение силы давления жидкости на всю пластинку:

.

Точное значение силы давления жидкости на пластинку определяется по формуле:

.

Следовательно, если учащиеся знакомы с понятием интеграла, сила давления жидкости на пластинку вычисляется по формуле

.

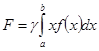Далее, если еще не было введено понятие (определенного) интеграла, следует переходить к рассмотрению этого понятия следующим образом. Итак, нами рассмотрены задачи (геометрическая и физические), решение которых производилось с помощью одной и той же последовательности действий (одним и тем же методом), приводящей к построению некоторой суммы и нахождению предела этой суммы. Так как указанный метод применяется к решению большого числа математических и прикладных задач, то, естественно изучить его, абстрагируясь от конкретного содержания задач. Сущность этого метода состоит в следующем:

1. Пусть на отрезке задана произвольная однозначная функция . Отрезок разбивается на частей одинаковой длины точками , причем .

2. На каждом из отрезков разбиения выбирается произвольная точка и для каждого отрезка разбиения составляется произведения значения функции в выбранной точке на длину соответствующего отрезка , т.е. произведение вида .

Статьи по теме:

Учебные достижения как измеряемый показатель качества в образовании
Для того чтобы система контроля эффективно воздействовала на образовательный процесс, необходимо выявление роли контроля в обучении и развитии личности. Поэтому понимание того, что мы измеряем и оцениваем, как анализируем и интерпретируем результаты педагогических измерений, является одним из важны ...

Формирование понятий экономии и бережливости у дошкольников через игровую деятельность
Сегодня перед Республикой Беларусь стоит важная задача – перестроить в сознании современного человека стереотип, что энергоресурсы неисчерпаемы и бесконечны, научить каждого личной ответственности за их экономическую трату. Уже с дошкольного возраста можно помочь ребенку усвоить азы бережного и заб ...

Диагностика художественных и творческих способностей в изобразительной деятельности детей дошкольного возраста
С образовательной точки зрения цель системы выявления творческих способностей у детей – достижение оптимального соответствия конкретной развивающей учебной программы психическим особенностям, потребностям, интересам определенной группы детей. На этапе обучения в течение года было проведено два срез ...