Методические рекомендации по решению задач с помощью определенного интеграла
.
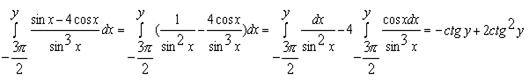Для удобства проведём вычисления по отдельности:
,
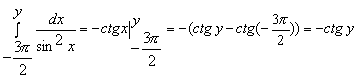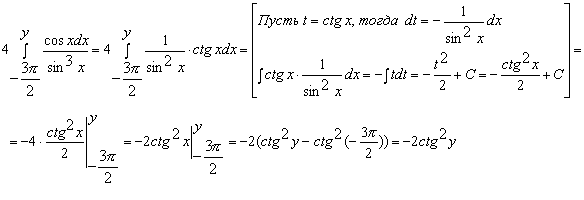
Приравнивая левую и правую часть равенства, получим:
.
Решая полученное тригонометрическое уравнение, имеем 
, где 
.
Но так как 
(по условию), то подбором устанавливаем, что 
.
Ответ: 
.
В данном задании учащимся приходится проводить исследовательскую работу с целью нахождения ОДЗ, решением тригонометрического уравнения, отбором корней. Здесь же они сталкиваются с вычислением нетабличного интеграла, для решения которого применяется подстановка, с которой многие учителя сталкиваются в своей преподавательской практике. Только правильный выбор подстановки и её использование приведёт к желаемому результату.
II. Решить неравенства.
А)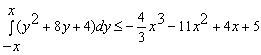 
,
Решение. Вычислим определённый интеграл:
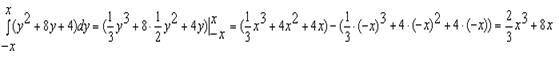
Тогда 
.Приравняем многочлен, стоящий в левой части к нулю и находим корни уравнения 
. Откуда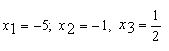 
. Методом интервалов решаем неравенство 
: откуда 
Ответ: 
.
Б)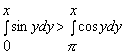 
.
Решение. По отдельности вычислим интеграл, стоящий в левой части и интеграл, стоящий в правой части неравенства:
; 
.
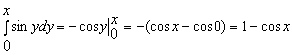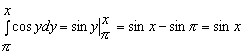Тогда
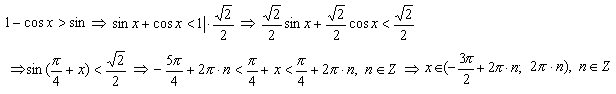
Ответ: 
.
Существенных трудностей задания А) и Б) не вызывают.
III. Оцените последовательности.
А)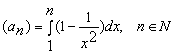 
,
Решение. Вычислим данный интеграл:
.
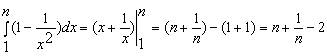Пользуясь неравенством Коши для двух неотрицательных чисел, оценим выражение
.
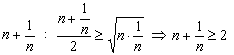Прибавив к обеим частям данного неравенства – 2, получим оценку (an):
.
Ответ: 
.
Б)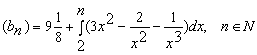 
.
Решение. Вычислим определённый интеграл:
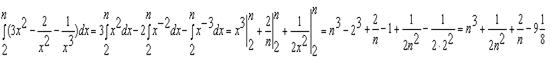
Тогда 
.
Используя неравенство Коши для трёх неотрицательных чисел, оценим (bn):
.
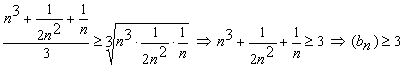Ответ: 
.
Статьи по теме:
Методы педагогического исследования образовательных потребностей
Под педагогической диагностикой понимаются все меры по освещению проблем и процессов в области педагогики, по измерению эффективности учебного процесса и успеваемости, по определению возможностей каждого в плане получения образования, особенно такие меры, которые служат принятию индивидуального реш ...
Организация исследования
и диагностика уровня эстетического развития старших дошкольников
Организация исследования. На 1 этапе осуществлялся: анализ психолого-педагогических источников по теме исследования; На 2 этапе проводился подбор методик для диагностики уровня эстетического развития. На 3 этапе проводилась экспериментальная работа по эстетическому воспитанию. Обобщались и системат ...
Валеологическое
направление учебно-воспитательного процесса
Валеологическое образование и воспитание (от лат. vale - будь здоров) - воспитание у учащихся потребности в здоровье, формирование у них научного понимания сущности здорового образа жизни и выработки соответствующего поведения. В основе Валеологического образования и воспитания лежит концепция форм ...