Методические рекомендации по решению задач с помощью определенного интеграла
Вся трудность заданий А) и Б) заключается лишь в том, на сколько хорошо учащиеся помнят неравенство Коши.
IV. На координатной плоскости изобразите множество точек (область), удовлетворяющих следующим условиям.
А) 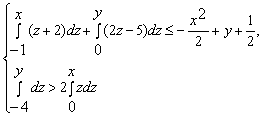
Решение. Преобразуем каждое неравенство системы по отдельности:
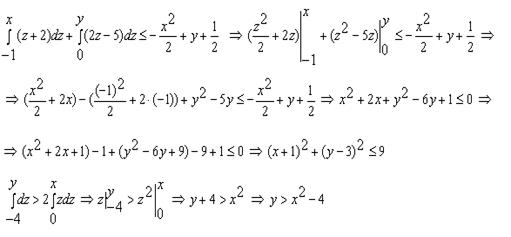 .
.
С учётом вычислений данная система примет вид: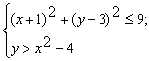
На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы:
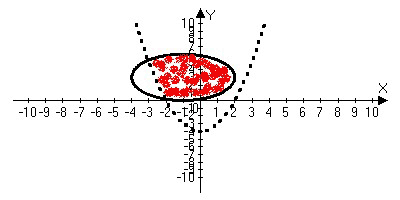
Закрашенная часть – искомая область.
Б) 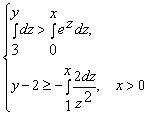
(данную конструкцию уместно предложить после изучения показательной функции).
Решение. Преобразуем каждое из неравенств системы по отдельности:
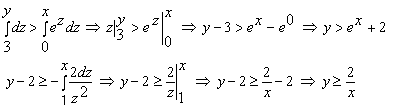
Тогда с учётом вычислений данная система примет вид:
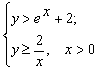 .
.
На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы:
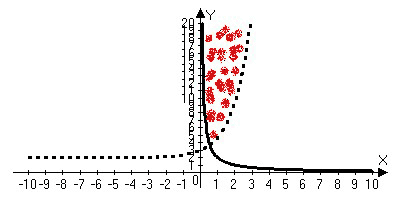
Закрашенная часть – искомая область.
Сложность заданий А) и Б) заключается лишь в том, на сколько правильно учащиеся могут решать неравенства с двумя переменными.
V. При всех значениях параметра решить уравнения.
А) 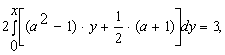
Решение. Для начала вычислим предложенный интеграл:
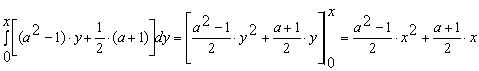 .
.
Тогда ![]() .
.
определенный интеграл задача
Решая данное уравнение относительно параметра а, имеем:
1. если a = – 1: – 3 = 0, сл., решений нет; если a = 1: получим линейное уравнение 2x – 3 = 0, сл., ![]() ;
;
2. если ![]()
2.1. если ![]() , то решений нет;
, то решений нет;
2.2. если
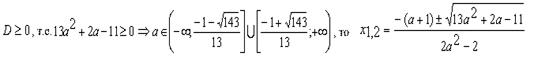
Произведя отбор, запишем ответ.
Ответ: при ![]() :
: 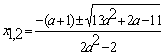
при ![]() : решений нет
: решений нет
при a = 1: ![]() .
.
Б). 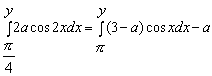
Решение. Вычислим предложенные определённые интегралы:
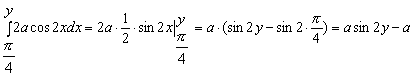 ;
;
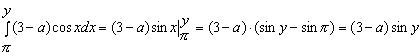 .
.
С учётом полученных вычислений имеем:
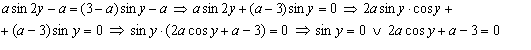
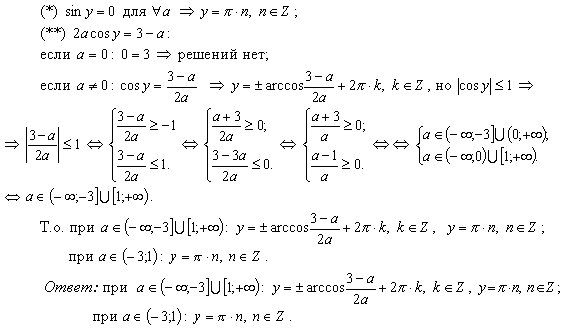
Во избежание ошибок при решении данного задания, необходимо заранее вспомнить с учащимися основные свойства тригонометрических функций (особенно области значений синуса и косинуса), а также правила решения отдельных задач с параметрами (это касается и задания А). Добиться максимальной работоспособности учащихся на уроке можно лишь при постановке таких проблемных ситуаций, которые будут создавать у школьников стремление их разрешить. На мой взгляд, одной из таких ситуаций будет использование предложенных конструкций, которые и осуществят творческий подход при обучении математике.
Статьи по теме:
Требования, предъявляемые к процессу
наблюдения
Наблюдение как метод исследования отличается от бытовой фиксации событий, что находит отражение в следующих требованиях к наблюдению. 1. Целенаправленность. В повседневной жизни, наблюдая окружающую действительность, человек фиксирует все, что попадает в поле его зрения, не ставя, как правило, пере ...
Разработка электронного образовательного ресурса
имя прилагательное образовательный ресурс Целью формирующего этапа эксперимента являлась разработка педагогических условий формирования понятия «имя прилагательное» у учеников 3-их классов и опыта организации деятельности с использованием цифровых образовательных ресурсов. На формирующем этапе иссл ...
Основные дидактические теории
Ассоциативная теория обучения. Ее методологические основания были заложены Дж. Локком и Я. А. Коменским. Данная теория базируется на следующих принципах: - всякое обучение опирается на чувственное познание: наглядные образцы важны постольку, поскольку обеспечивают продвижение сознания к обобщениям; ...

