Методические рекомендации по решению задач с помощью определенного интеграла

Необходимо повторить основные понятия интеграла, вспомнить: основные способы и методы решения определенного интеграла в зависимости от его вида. А затем плавно перейти к изложению нового материала.

Рассмотрим интеграл, применяя формулу Ньютона-Лейбница. В подинтегральном выражении находим первообразную, а затем вместо неизвестного подставляем пределы интегрирования.

А сейчас рассмотрим пример, который поможет осмыслить выше сказанное.

Пример 1

.

Решение.

Поскольку для x одной из первообразных является ,

III. Первичное осмысление и закрепление нового материала через практику (учащиеся работают у доски).

Пример 2

Решение.

.

Пример 3

.

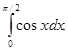Решение.

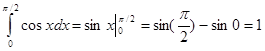
Пример 4

.

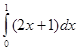Решение.

.

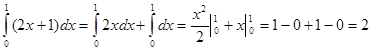IV. Постановка домашнего задания.

Продиктовать примеры три - четыре (использовать материал, содержащийся в приложении).

V. Подведение итогов.

Ребята, сегодня мы познакомились с определенными интегралами, сводящиеся к формуле Ньютона-Лейбница, а также узнали способы их решения. Есть что-нибудь непонятное в этой теме?

Если есть, то учитель ещё раз повторяет непонятные положения.

Урок №3

Тема урока:

Свойства определенного интеграла.

Тип урока:

Повторение изученного материала.

Цели урока:

1. Образовательная:

-повторить свойства определенного интеграла;

- рассмотреть способы решения определенного интеграла, сводящегося к формуле Ньютона-Лейбница.

2. Развивающая:

- развивать память учащихся;

- развивать логическое и абстрактное мышление.

3. Воспитательная

- прививать интерес к математике;

- воспитывать положительное отношение к процессу обучения.

Ход урока

I. Организационный момент:

- приветствие класса;

- проверить готовность класса к уроку;

- сообщить тему урока и цели.

II.Устный опрос по теории.

- Сформулируйте основную теорему.

- Что называется определенным интегралом?

- Как найти значение определенного интеграла?

III. Укажем свойства определенного интеграла (выражаемые равенствами) используемые далее в упражнениях. Будем считать, что функции, о которых пойдет речь, имеют первообразные на отрезках, где они рассматриваются.

1. .

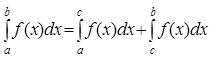2.

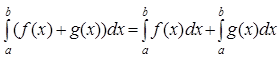
- определенный интеграл от суммы двух функций равен сумме определенных интегралов от этих функций.

3. ,

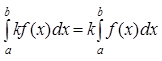k=const-постоянный множитель можно выносить за знак определенного интеграла.

Очевидным следствием свойств 2 и 3 является соотношение

,

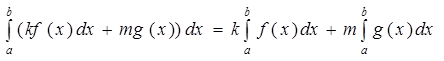k=const, m=const- определенный интеграл от линейной комбинации функций равен соответствующей линейной комбинации определенных интегралов от этих функций.

Статьи по теме:

Понятие, основные причины и формы ДЦП
Термин детский церебральный паралич впервые был введен Зигмундом Фрейдом в 1893 г. Детский церебральный паралич тяжелое заболевание головного мозга, проявляющееся в различных психомоторных нарушениях при ведущем двигательном дефекте. Термин детский церебральный паралич (ДЦП) обозначает группу двига ...

Место гимнастики в педагогической системе физического воспитания
Гимнастика – одно из действенных и универсальных средств физического воспитания, применяемое с целью образования, спортивной подготовки, оздоровления, восстановления, лечения, приобретения жизненно необходимых навыков прикладного, производственного или оборонного значения. Она является хорошим сред ...

Основные педагогические идеи Джона Дьюи
1. Накопление детьми личного опыта стоит выше овладения систематизированными научными знаниями. Усвоение знаний – есть стихийный, неуправляемый процесс. Учение в педагогической системе прагматистов имеет дело с выработкой личных идей и понятий. Учение происходит только тогда, когда что-то случается ...