Методические рекомендации по решению задач с помощью определенного интеграла

Ребята приступают к самостоятельной работе. Тот, кто выполнит все задания первым, подходит к учителю, который быстро проверяет работу ученика и выставляет за нее оценку. Несколько человек, получившие хорошие оценки, объявляются консультантами. Они должны проверить работы своих товарищей и выставить в их тетрадях свои оценки. Разрешение на выставление оценок мобилизует проверяющих. Они с большой ответственностью приступают к проверке. Учитель же может проконтролировать проверяющих, собрав тетради и просмотрев их после урока.

Такие уроки требуют от учителя максимума внимания и умения владеть классом, но и учащимся они приносят большую пользу как в учебном, так и в воспитательном плане.

Система упражнений для изучения интеграла в учебном пособии недостаточно совершенна. Задания здесь в основном сводятся к вычислению площадей фигур и интеграла, т.е. имеют тренировочный характер. На уроках в 10 классе будут полезны задачи, в которых вычислению интеграла предшествовало бы упрощение или преобразование формулы, задающей функцию. Таковы следующие задачи:

1. Вычислите интеграл, предварительно выполнив необходимые преобразования подынтегральной функции:

а) ;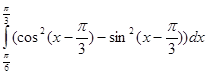

б) ;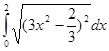

в) .

Дополнительного времени, как и дополнительных знаний, для рассмотрения приведенных задач фактически не требуется: их решение целесообразно связать с повторением.

Можно предлагать и такие задачи на вычисления интегралов, которые требуют более сложных преобразований тригонометрических выражений.

2. Вычислите интеграл:

а) ;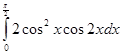

б) ;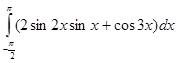

в) :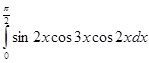

Решение.

.

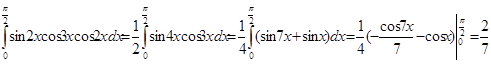Задачи 1-2 полезно рассмотреть на внеклассных и факультативных занятиях.

До сих пор рассматривались упражнения, в которых требовалось вычислить интеграл, привлекая для этого сведения из предшествующего курса алгебры и начал анализа. Но и задачам, в которых интеграл играет вспомогательную роль, надо отвести время на уроках или внеклассных занятиях. Вот примеры таких упражнений.

3.Решить уравнение:

а) ; б) ;

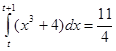4. Найти все значения t такие, что и является корнем уравнения:

а) 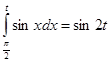; б) .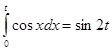

5. Найти множество неотрицательных корней уравнения:

.

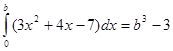Предложенные задачи, несомненно, будут способствовать сознательному усвоению понятия интеграла. Необходимо предупреждать возможность формального подхода к вычислению интегралов. Прежде чем вычислять интеграл, нужно убедиться, что на отрезке интегрирования существует первообразная подынтегральной функции: формула Ньютона-Лейбница применима лишь для непрерывных функций, а они имеют первообразную. Чтобы избежать недоразумений, полезно приучать десятиклассников перед формальным интегрированием устанавливать, непрерывна ли заданная (под интегралом) функция. В этих целях полезно рассмотреть следующую задачу:

Статьи по теме:

Методы самовоспитания личности
В основе самовоспитания лежит принцип опережающего отражения в сознании человека тех действий и поступков, которые он собирается совершить, определение тех черт и качеств, которые он предполагает выработать у себя. Если подобная «мысленная программа» формируется, она побуждает личность к практическ ...

Развитие двигательной памяти у старших дошкольников
Данные психолого-педагогической диагностики детей с фонетико-фонематическим недоразвитием речи позволяют специалистам определить наиболее адекватную систему организации детей в процессе обучения, найти для каждого ребенка наиболее подходящие индивидуальные методы и приемы коррекции. Правильно подоб ...

Личностно-деятельностный подход с позиции педагога
В самой общей форме личностно-деятельностный подход в совокупности его компонентов (и особенно личностного) означает с позиции обучающего организацию и управление целенаправленной учебной деятельностью ученика в «общем контексте его жизнедеятельности — направленности интересов, жизненных планов, це ...