Методические рекомендации по решению задач с помощью определенного интеграла

Изучение темы "Определенный интеграл" представляет собой сложный процесс, основными компонентами которого являются:

- приобретение учащимися определенной системы знаний, умений, навыков;

- овладение определенной системой фактов, идей.

Целью занятий по решению определенного интеграла является расширение и углубление знаний, развитие интереса учащихся к предмету, а также развитие их математических способностей, формирование у учащихся понятий и методов решения систем уравнений различной сложности.

Положение школьного курса алгебры в системе математических предметов имеет свою специфику. Прежде всего, курс алгебры девятилетней школы, по своему содержанию, носит преимущественно прикладной и практический характер. При его изучении учащиеся овладевают определенными знаниями, умениями и навыками, составляющими существенное звено математического аппарата, который активно применяется при решении разнообразных математических и нематематических задач. При этом следует отметить то, что обучение в VII -IX классе представляет не завершающий, а промежуточный этап в системе математического образования каждого школьника. На базе, полученной учеником математической подготовки, строится его дальнейшее обучение в X – XI классах. В XI классе вводится понятие определенного интеграла, и рассматриваются методы его решения.

Исходя из вышесказанного, следует отметить, важность изучения темы «Определенный интеграл». Основное место в данной теме занимают методы решения интеграла; замена переменной и интегрирование по частям.

Как же сконцентрировать внимание учащихся при изучении определенного интеграла? Эту проблему можно решать разными способами. При закреплении и тренировке в применении изученного материала полезен следующий прием. После предъявления первого задания учитель, не решая и не разъясняя его, просит учащихся составить аналогичное упражнение. Уже одно это заставляет школьников сосредоточиться, так как понять аналогию можно только тогда, когда хорошо проанализировал условие исходного примера.

Рассмотрим урок, на котором отрабатывается метод решения определенного интеграла способом подстановки. Учащимся предлагается вычислить следующий интеграл:

.

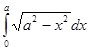Решение. Воспользуемся подстановкой , роль и играют значения 0 и . Имеем

.

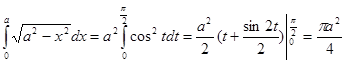Это задание ученики должны выполнить самостоятельно. При этом они имеют право задавать учителю вопросы по поводу возникающих трудностей.

Следующее задание уже более сложнее. Например:

.

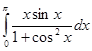Решение. Подстановка (где t изменяется от до 0) приводит к равенству

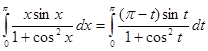или

.

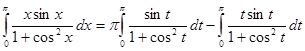Перенося последний интеграл налево, получаем

.

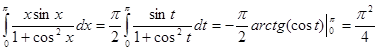Описанный метод очень удобен для рассмотрения различных случаев вычисления интегралов. Описанная работа занимает обычно весь урок. Естественно, что более сильные учащиеся опережают класс. Для того чтобы они не дезорганизовывались, ожидая новых заданий, учитель предлагает им решать упражнения из учебника. Можно отметить и еще один недостаток таких уроков. Учащиеся одного и того же класса в одно и то же время распадаются на две большие группы, которым нет дела друг до друга. Такое отчуждение вредно влияет на внимание учащихся. Объединить класс можно несколько иным построением урока. Учитель вначале рассматривает не одно задание, а сразу два или три. Разъяснив задание, он стирает его с доски. Закончив объяснения, учитель составляет на доске три задания для самостоятельной работы.

Статьи по теме:

Содержание понятия «предматематическое развитие и подготовка дошкольников». Основные задачи предматематической подготовки дошкольников
Предматематическое развитие дошкольника предусматривает знакомство дошкольника с математических категориями (счеты, числа, геометрические фигуры и обьекты, их количества и разнообразие форм) через процесс общения, познавательно-практическую, художественную, учебно-игровую, тематическую деятельность ...

Особенности мышления младших школьников
Мышление совершается по законам, общим для всех людей, вместе с тем в мышлении проявляются возрастные и индивидуальные особенности человека. Что касается мышления младшего школьника, то оно тесно связанное с чувственным познанием мира. Изучение развития мышления ребенка представляет собой большой т ...

Психологические особенности детей младшего школьного возраста
Младший школьный возраст (от 7 до 11 лет) называют вершиной детства. Ребенок сохраняет много детских качеств – легкомыслие, наивность, взгляд на взрослого снизу вверх. Но он уже начинает утрачивать детскую непосредственность в поведении, у него появляется другая логика мышления. Учение для него – з ...